The purpose of this post is to illustrate and define the concept of probability in terms of possibilities.

Take a look at the following binary tree. It depicts the possible outcomes of three successive coin flips of a coin with the sides showing 0 and 1.

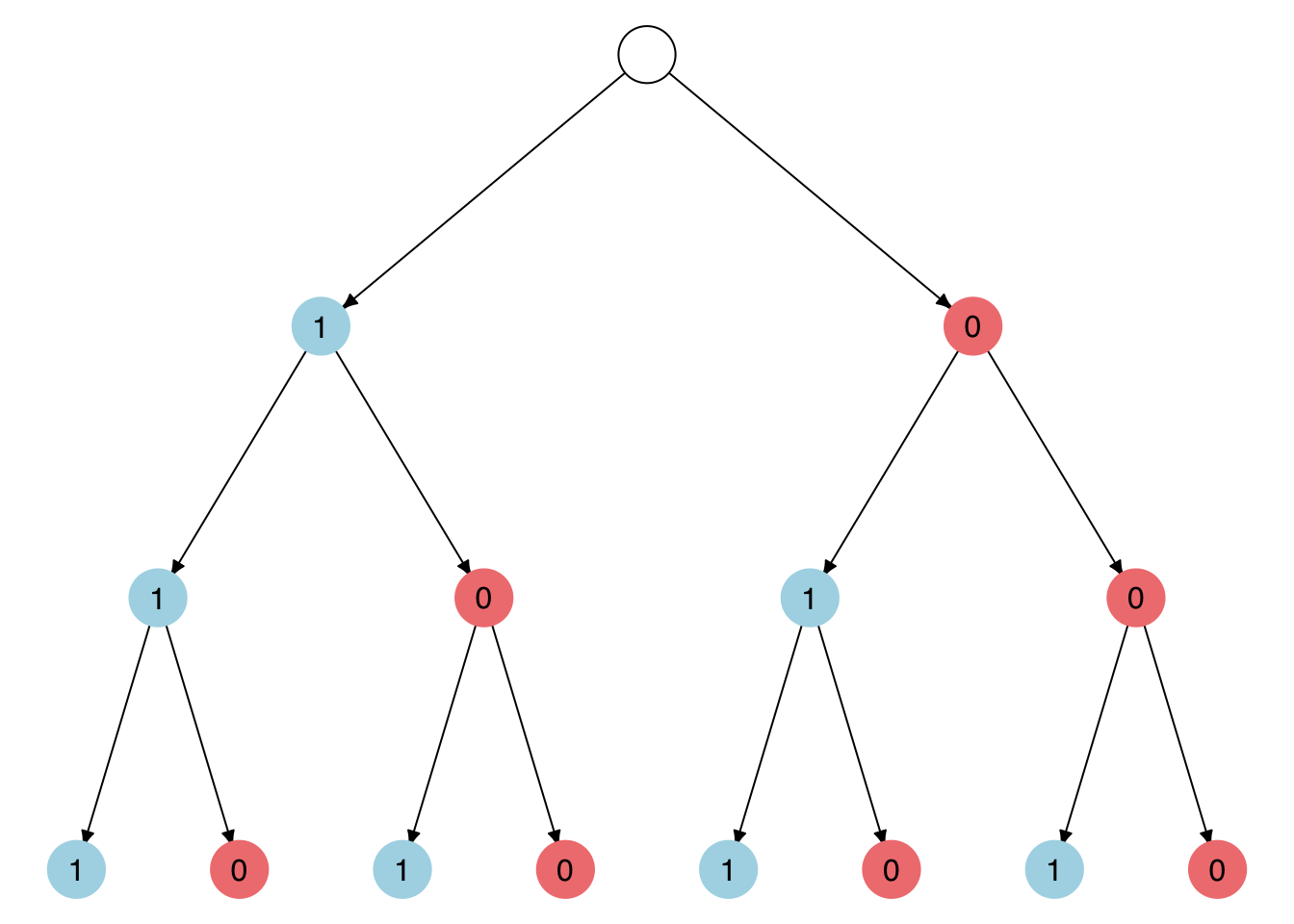
threeFlips

Assuming the coin is fair, different arrangements of results may vary in the number of possible ways in which they could happen.
For instance, having two 1s and one 0 as the outcome of three coin flips can be realized by the following highlighted paths:

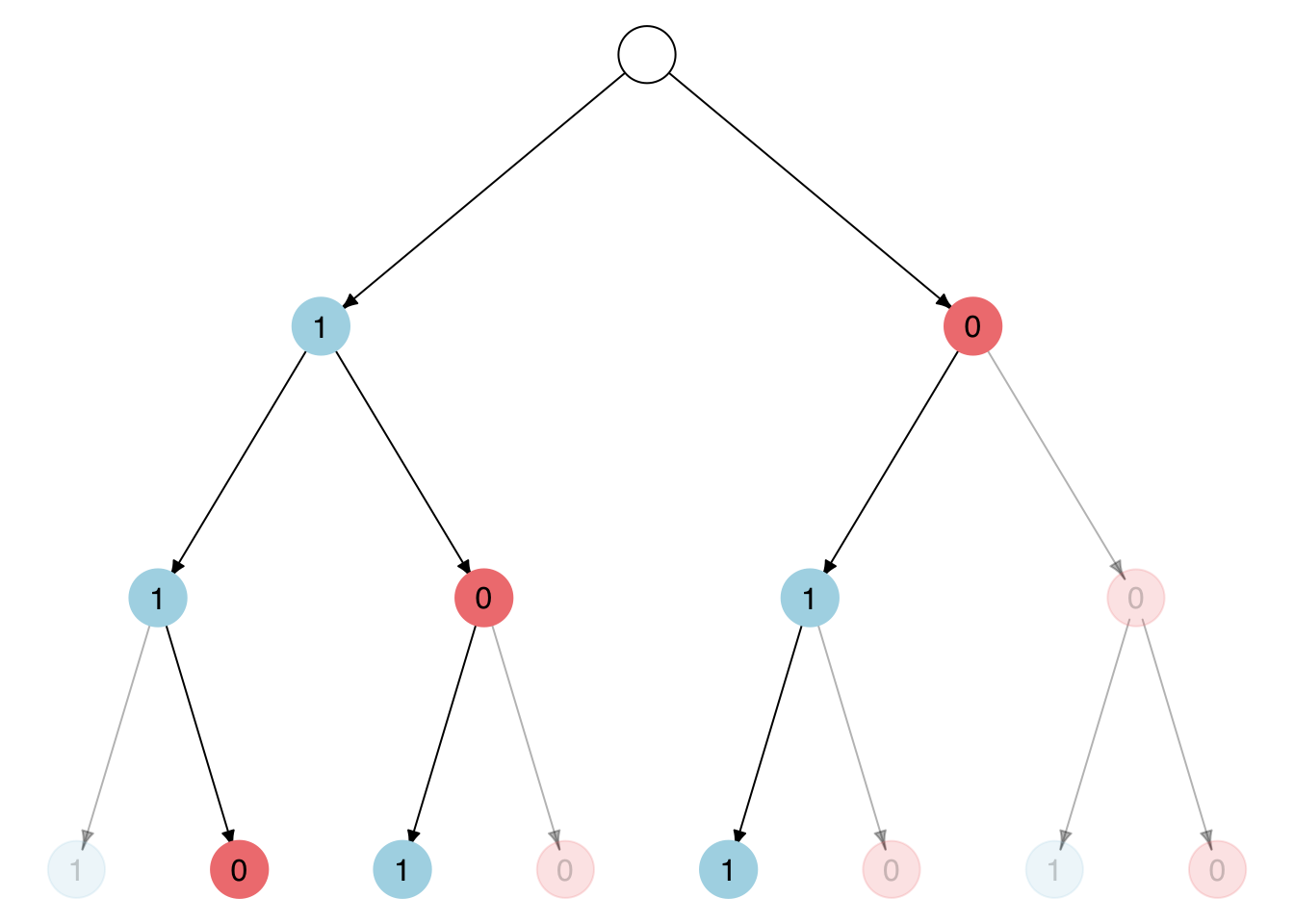
threeFlipsEvent

Three out of eight possible paths can realize this outcome. In contrast, only one out of eight possible paths can realize three 1s and zero 0s.

We use the term probability to describe such possibility ratios. Specifically the probability of an event corresponds to the relative number of possible ways in which it could be realized. In that sense, for a fair coin the probability of the (1, 1, 0) event in which the order is irrelevant is 3/8.

Biased paths

The above example used a fair coin and a binary tree. But what would the probability of an event be in case of a biased coin?

As an example we take a coin that lands showing 1 in only one out of four cases and shows 0 otherwise.
In a graph, the possible outcomes of two successive coin flips with such a coin could be illustrated as follows:

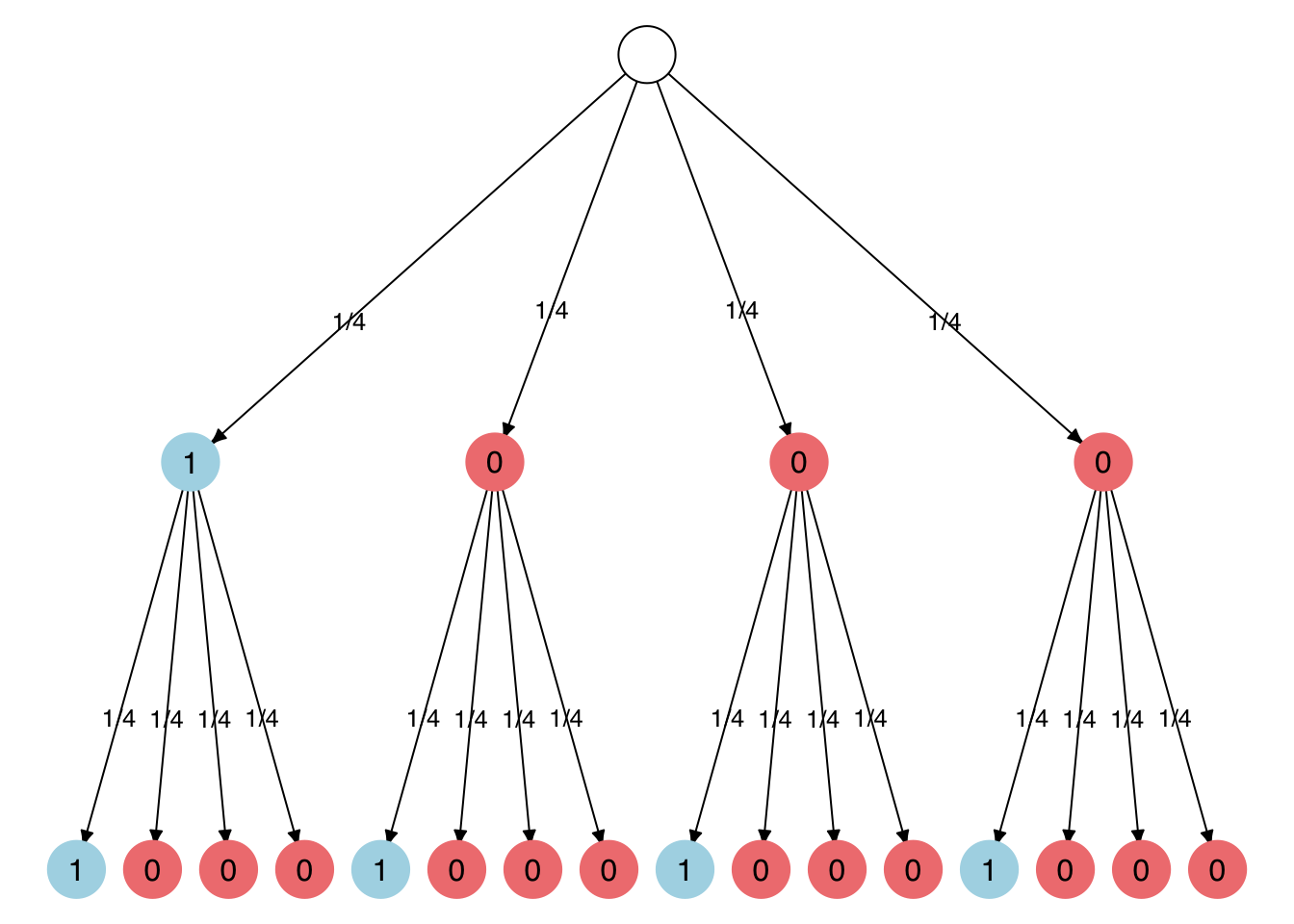
biased

The new graph is no longer binary but the above definition of probability still applies.
For instance, the probability of having one 1 and one 0 after two coin tosses is 6/16 = 0.375, i.e. the number of paths that can realize the event (1,0) divided by the number of all possible paths.

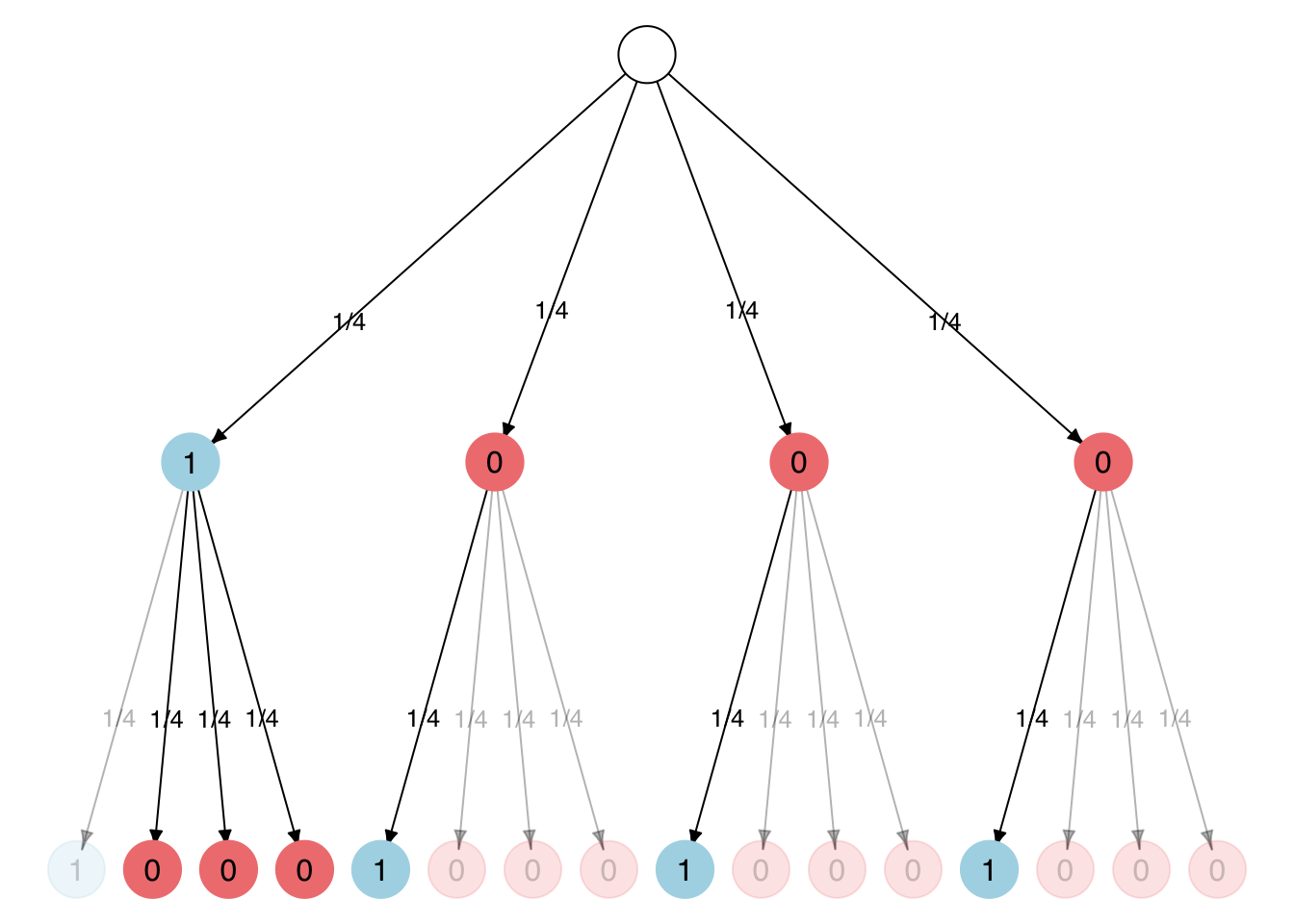
biasedEvent

Conveniently, this can be represented as binary tree in which each individual edge is directly labeled with the relative number of ways in which it could happen (i.e. it’s probability). In this summarized representation the probability of an event can simply be obtained by multiplying the probabilities within each path and taking the sum of such products of all possible paths as the probability of an event.

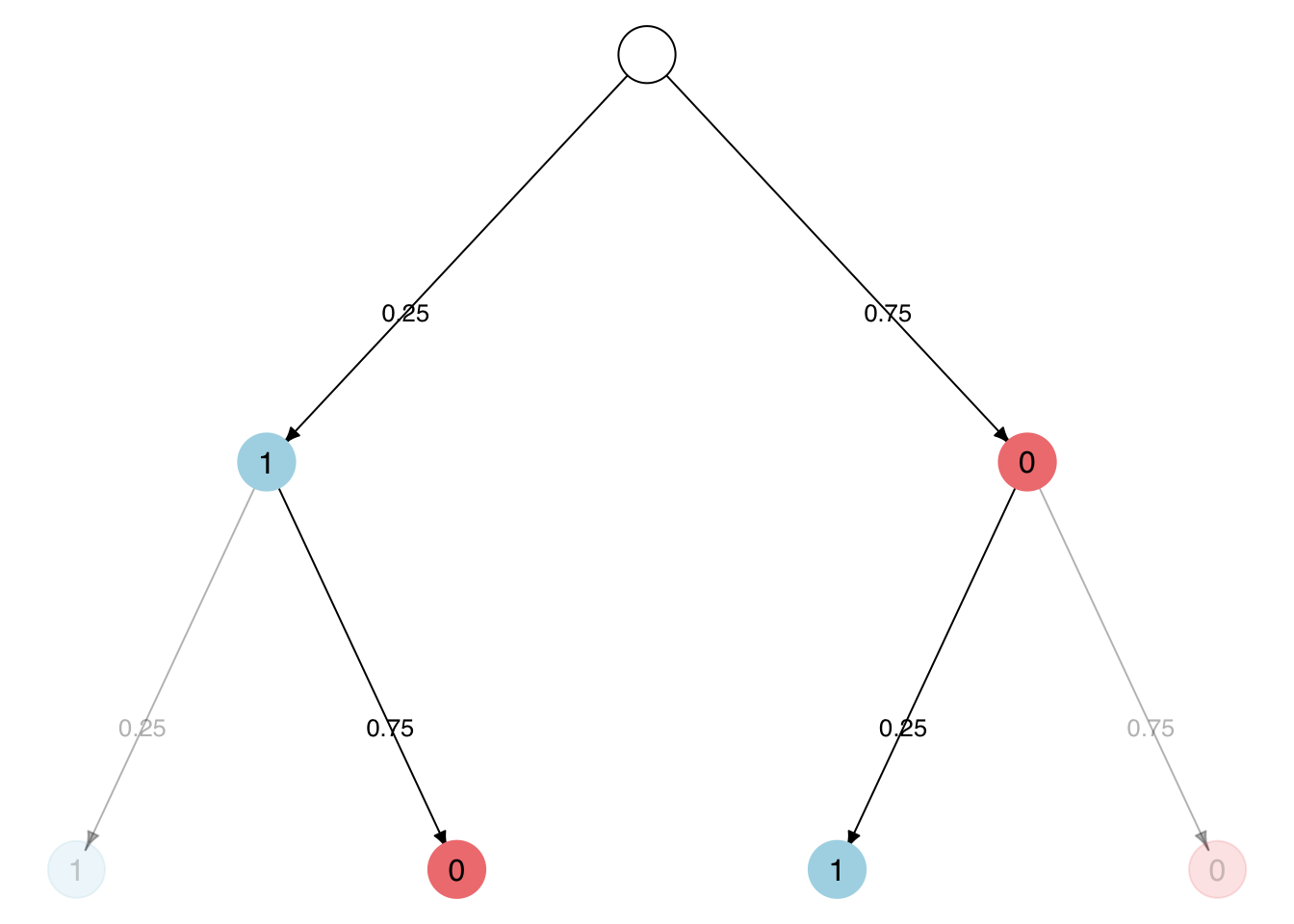
biasedBinary

For the event (1,0) where 0 is three times as likely as 1 this would correspond to:
0.25 * 0.75 + 0.75 * 0.25 = 2 * (0.75 * 0.25) = 0.375

Feel free to take a look at what I wrote about coins if you also want to learn about binomial probability distributions.